What are the laws of exponents in real numbers for Prep 2?

The main laws of exponents for Prep 2 include rules for multiplication, division, power of a power, zero exponents, and negative exponents. These rules help simplify expressions involving powers of real numbers.

How do you multiply powers with the same base?

To multiply powers with the same base, you keep the base and add the exponents. The rule is: a^m × a^n = a^(m+n).

What is the rule for negative exponents?

A negative exponent indicates the reciprocal of the base raised to the positive exponent. The rule is: a^(-n) = 1 / a^n, where a is not zero.

ما هي قوانين الأسس في الأعداد الحقيقية للصف الثاني الإعدادي؟

قوانين الأسس الرئيسية للصف الثاني الإعدادي تشمل قواعد لضرب وقسمة القوى، قوة القوة، الأس الصفري، والأسس السالبة. هذه القواعد تساعد في تبسيط المقادير التي تحتوي على قوى لأعداد حقيقية.

كيف تضرب القوى التي لها نفس الأساس؟

لضرب القوى التي لها نفس الأساس، نحتفظ بالأساس ونجمع الأسس. القاعدة هي: أ^م × أ^ن = أ^(م+ن).

ما هي قاعدة الأسس السالبة؟

الأس السالب يعني المعكوس الضربي للأساس مرفوعاً للأس الموجب. القاعدة هي: أ^(-ن) = ١ / أ^ن، حيث أ لا تساوي صفراً.

Laws of Exponents in Real Numbers | Math Egypt

📖 Learn!

📚 Repeated Multiplication in the Set of Real Numbers

The mathematical expression $a^n$ is used to represent the product of multiplying the real number $a$ by itself $n$ times.

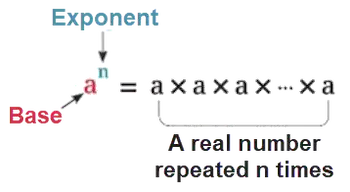
Diagram showing a^n equals a multiplied by itself n times, with 'a' as the base and 'n' as the exponent. From Math Egypt by Mr. Ayman Hassan

For example:

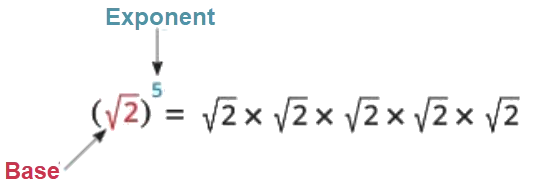
Example showing rules for negative bases with even and odd exponents. If n is an even integer, then (-a)^n = a^n. If n is an odd integer, then (-a)^n = -a^n. From Math Egypt by Mr. Ayman Hassan

📝 Example (1)

Find the value of each of the following:

1$(-\sqrt{5})^4$

2$ -(\sqrt{5})^4 $

3$(-\sqrt{5})^3$

4$(-\sqrt{2})^5$

5$ -(\sqrt{2})^5 $

6$(-\sqrt{2})^6$

Solution

$(-\sqrt{5})^4$ $ = (\sqrt{5})^4$ (Since the exponent is even) $ = (\sqrt{5}^2)^2 = 5^2 $ $ = 25 $

$ -(\sqrt{5})^4 $ $ = - (5^2) $ (Calculate the power first) $ = -25 $

$(-\sqrt{5})^3$ $ = -(\sqrt{5})^3$ (Since the exponent is odd) $ = -(\sqrt{5} \times \sqrt{5} \times \sqrt{5}) $ $ = -5\sqrt{5} $

$(-\sqrt{2})^5$ $ = -(\sqrt{2})^5$ (Since the exponent is odd) $ = -(\sqrt{2}^2 \times \sqrt{2}^2 \times \sqrt{2}) $ $ = -(2 \times 2 \times \sqrt{2}) = -4\sqrt{2} $

$ -(\sqrt{2})^5 $ $ = -(4\sqrt{2}) $ (Calculate the power first) $ = -4\sqrt{2} $

$(-\sqrt{2})^6$ $ = (\sqrt{2})^6$ (Since the exponent is even) $ = (\sqrt{2}^2)^3 = 2^3 $ $ = 8 $

Zero and Negative Exponents

The Zero Exponent

Any non-zero real number raised to the power of zero equals 1.

$ a^0 = 1 $, where $ a \in \mathbb{R}^* $

Examples: $ 5^0 = 1 $, $ (\sqrt{3})^0 = 1 $, $ (-\sqrt[3]{4})^0 = 1 $

The Negative Exponent

For any non-zero real number $ a $ and a positive integer $ n $, the expression $ a^{-n} $ is the multiplicative inverse of $ a^n $.

$ a^{-n} = \frac{1}{a^n} $, where $ a \in \mathbb{R}^* $, $ n \in \mathbb{Z}^+ $

Examples:

$ (\sqrt{3})^{-4} = \frac{1}{(\sqrt{3})^4} = \frac{1}{9} $

$ (\frac{1}{\sqrt[3]{4}})^{-3} = (\sqrt[3]{4})^3 = 4 $

Important Note

💡

Division by Zero

Division by zero is undefined. Therefore, when symbols are present in the denominator, it is a condition that these symbols must not equal zero.

This means for any expression of the form $\frac{X}{Y}$, $Y \neq 0$.

Laws of Multiplication

Rule 1: Product of Powers with the Same Base

When multiplying powers with the same base, keep the base and add the exponents. For any real number $a \in \mathbb{R}$ and integers $m, n \in \mathbb{Z}$:

$ a^m \times a^n = a^{m+n} $

Examples:

$ 2^4 \times 2^6 = 2^{4+6} = 2^{10} $
$ a^{-3} \times a^5 = a^{-3+5} = a^2 $

Rule 2: Power of a Product

When finding the power of a product of two numbers, distribute the exponent to each number. For any real numbers $a, b \in \mathbb{R}$ and integer $n \in \mathbb{Z}$:

$ (a \times b)^n = a^n \times b^n $

Example:

$ (3\sqrt{2})^2 = 3^2 \times (\sqrt{2})^2 = 9 \times 2 = 18 $

Important Note: Sum/Difference of Powers

It is important to remember that the exponent cannot be distributed over addition or subtraction:

⚠️ $ (a+b)^n \neq a^n + b^n $
⚠️ $ (a-b)^n \neq a^n - b^n $

Laws of Division

Rule 1: Quotient of Powers with the Same Base

When dividing powers with the same base, keep the base and subtract the exponents. For any non-zero real number $a \in \mathbb{R}^*$ and integers $m, n \in \mathbb{Z}$:

$ \frac{a^m}{a^n} = a^{m-n} $

Example:

$ \frac{(\sqrt{7})^5}{(\sqrt{7})^2} = (\sqrt{7})^{5-2} = (\sqrt{7})^3 = 7\sqrt{7} $

Rule 2: Power of a Quotient

When finding the power of a quotient of two numbers, distribute the exponent to both the numerator and the denominator. For any real number $a \in \mathbb{R}$, non-zero real number $b \in \mathbb{R}^*$, and integer $n \in \mathbb{Z}$:

$ (\frac{a}{b})^n = \frac{a^n}{b^n} $

Example:

$ (\frac{6}{\sqrt{3}})^2 = \frac{6^2}{(\sqrt{3})^2} = \frac{36}{3} = 12 $

📝 Example (2)

Simplify each of the following to its simplest form:

1$ \frac{(6a)^2}{2a} $

2$ \frac{(-\sqrt{3}ab)^4}{3a^4b^2} $

3$ \frac{(\sqrt{8})^4 \times (\sqrt{2})^3}{(2\sqrt{2})^5} $

4$ \frac{(\sqrt{3})^2 \times (\sqrt{3})^4 \times (\sqrt{3})^{-1}}{(\sqrt{3})^5 \times (\sqrt{3})^{-2}} $

5$ \frac{(\sqrt{18})^5 \times (\sqrt{2})^3}{(\sqrt{12})^4} $

Solution

$ \frac{(6a)^2}{2a} $ $ = \frac{6^2 \times a^2}{2 \times a} = \frac{36a^2}{2a} $ $ = 18a^{2-1} = 18a $

$ \frac{(-\sqrt{3}ab)^4}{3a^4b^2} $ $ = \frac{(-\sqrt{3})^4 \times a^4 \times b^4}{3 \times a^4 \times b^2} $ $ = \frac{9 \times a^4 \times b^4}{3 \times a^4 \times b^2} $ $ = 3 \times a^{4-4} \times b^{4-2} $ $ = 3 \times a^0 \times b^2 $ $ = 3 \times 1 \times b^2 = 3b^2 $

$ \frac{(\sqrt{8})^4 \times (\sqrt{2})^3}{(2\sqrt{2})^5} $ $ = \frac{(\sqrt{4 \times 2})^4 \times (\sqrt{2})^3}{(2\sqrt{2})^5} = \frac{(2\sqrt{2})^4 \times (\sqrt{2})^3}{(2\sqrt{2})^5} $ $ = \frac{2^4 \times (\sqrt{2})^4 \times (\sqrt{2})^3}{2^5 \times (\sqrt{2})^5} $ $ = 2^{4-5} \times (\sqrt{2})^{4+3-5} $ $ = 2^{-1} \times (\sqrt{2})^2 $ $ = \frac{1}{2} \times 2 = 1 $

$ \frac{(\sqrt{3})^2 \times (\sqrt{3})^4 \times (\sqrt{3})^{-1}}{(\sqrt{3})^5 \times (\sqrt{3})^{-2}} $ $ = \frac{(\sqrt{3})^{2+4+(-1)}}{(\sqrt{3})^{5+(-2)}} $ $ = \frac{(\sqrt{3})^{5}}{(\sqrt{3})^{3}} $ $ = (\sqrt{3})^{5-3} $ $ = (\sqrt{3})^2 $ $ = 3 $

$ \frac{(\sqrt{18})^5 \times (\sqrt{2})^3}{(\sqrt{12})^4} $ $ = \frac{(3\sqrt{2})^5 \times (\sqrt{2})^3}{(2\sqrt{3})^4} $ $ = \frac{3^5 \times (\sqrt{2})^5 \times (\sqrt{2})^3}{2^4 \times (\sqrt{3})^4} $ $ = \frac{3^5 \times (\sqrt{2})^{5+3}}{2^4 \times (\sqrt{3})^4} $ $ = \frac{3^5 \times (\sqrt{2})^8}{2^4 \times (\sqrt{3})^4} $ $ = \frac{3^5 \times 2^4}{2^4 \times 3^2} $ $ = 3^{5-2} \times 2^{4-4} $ $ = 3^3 \times 2^0 $ $ = 27 \times 1 $ $ = 27 $

📝 Example (3)

Simplify each of the following to its simplest form, then find the numerical value for the given value of $n$:

1$ (\sqrt{6})^n \times (\sqrt{3})^{n-1} \times (\sqrt{2})^{-n} $, then find the numerical value when $n=1$.

2$ \frac{10^{2n} \times 0.001}{10^{-n+1} \times 100} $, then find the numerical value when $n=2$.

3$ \frac{(\sqrt{5})^n \times (\sqrt{3})^{2-n}}{3 \times (\sqrt{15})^{-n}} $, then find the numerical value when $n=-2$.

4$ \frac{1000 \times 0.1^n \times 10^{n-1}}{10^{n+2}} $

Solution

$ (\sqrt{6})^n \times (\sqrt{3})^{n-1} \times (\sqrt{2})^{-n} $ $ = (\sqrt{3} \times \sqrt{2})^n \times (\sqrt{3})^{n-1} \times (\sqrt{2})^{-n} $ $ = (\sqrt{3})^n \times (\sqrt{2})^n \times (\sqrt{3})^{n-1} \times (\sqrt{2})^{-n} $ $ = (\sqrt{3})^{n+n-1} \times (\sqrt{2})^{n-n} $ $ = (\sqrt{3})^{2n-1} \times (\sqrt{2})^0 $ $ = (\sqrt{3})^{2n-1} \times 1 $ $ = (\sqrt{3})^{2n-1} $

When $n=1$:

$ \therefore (\sqrt{3})^{2(1)-1} = (\sqrt{3})^{2-1} = \sqrt{3} $

$ \frac{10^{2n} \times 0.001}{10^{-n+1} \times 100} $ $ = \frac{10^{2n} \times 10^{-3}}{10^{-n+1} \times 10^2} $ $ = \frac{10^{2n-3}}{10^{-n+1+2}} $ $ = \frac{10^{2n-3}}{10^{-n+3}} $ $ = 10^{(2n-3) - (-n+3)} $ $ = 10^{2n-3+n-3} $ $ = 10^{3n-6} $

When $n=2$:

$ \therefore 10^{3(2)-6} = 10^{6-6} = 10^0 = 1 $

$ \frac{(\sqrt{5})^n \times (\sqrt{3})^{2-n}}{3 \times (\sqrt{15})^{-n}} $ $ = \frac{(\sqrt{5})^n \times (\sqrt{3})^{2-n}}{3 \times (\sqrt{5} \times \sqrt{3})^{-n}} $ $ = \frac{(\sqrt{5})^n \times (\sqrt{3})^{2-n}}{3 \times (\sqrt{5})^{-n} \times (\sqrt{3})^{-n}} $ $ = \frac{1}{3} \times (\sqrt{5})^{n - (-n)} \times (\sqrt{3})^{(2-n) - (-n)} $ $ = \frac{1}{3} \times (\sqrt{5})^{2n} \times (\sqrt{3})^{2-n+n} $ $ = \frac{1}{3} \times ((\sqrt{5})^2)^n \times (\sqrt{3})^2 $ $ = \frac{1}{3} \times 5^n \times 3 $ $ = 5^n $

When $n=-2$:

$ \therefore 5^{-2} = \frac{1}{5^2} = \frac{1}{25} $

$ \frac{1000 \times 0.1^n \times 10^{n-1}}{10^{n+2}} $ $ = \frac{10^3 \times (10^{-1})^n \times 10^{n-1}}{10^{n+2}} $ $ = \frac{10^3 \times 10^{-n} \times 10^{n-1}}{10^{n+2}} $ $ = \frac{10^{3-n+n-1}}{10^{n+2}} $ $ = \frac{10^{2}}{10^{n+2}} $ $ = 10^{2 - (n+2)} $ $ = 10^{2 - n - 2} $ $ = 10^{-n} $

There is no specific value of $n$ given for this problem, so the simplified form is $10^{-n}$.

📝 Example (4)

In the opposite figure:

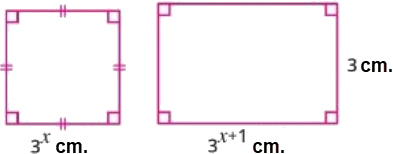
Image showing a square with side length 3^x cm and a rectangle with dimensions 3^(x+1) cm and 3 cm. From Math Egypt by Mr. Ayman Hassan

A square with side length $3^x$ cm.
A rectangle with dimensions $3^{x+1}$ cm and $3$ cm.

If the perimeter of the square is 20 cm, then find the area of the rectangle.

Solution

Perimeter of the square $ = 20 $ cm

$ \therefore 4 \times 3^x = 20 $ $ \therefore 3^x = \frac{20}{4} = 5 $

Area of the rectangle $A = \text{Length} \times \text{Width}$

$ \therefore A = 3^{x+1} \times 3^x $ $ = 3^{x+1+x} = 3^{2x+1} $ $ = 3^{2x} \times 3^1 $ $ = (3^x)^2 \times 3 $ $ = (5)^2 \times 3 $ (Substitute $3^x=5$) $ = 25 \times 3 $ $ = 75 $

Area of the rectangle $ = 75 \text{ cm}^2 $

📝 Example (5)

If $3^x = 4$, then find the numerical value for each of the following:

1$ 3^{x+1} $

2$ 3^{x-1} $

3$ 3^{x+2} + 3^{x+3} $

Solution

$ 3^{x+1} $ $ = 3^x \times 3^1 $ $ = 4 \times 3 $ (Substitute $3^x=4$) $ = 12 $

$ 3^{x-1} $ $ = 3^x \times 3^{-1} $ $ = 3^x \times \frac{1}{3} $ $ = 4 \times \frac{1}{3} $ (Substitute $3^x=4$) $ = \frac{4}{3} $

$ 3^{x+2} + 3^{x+3} $ $ = 3^x \times 3^2 + 3^x \times 3^3 $ $ = 3^x (3^2 + 3^3) $ (Factor out $3^x$) $ = 4 (9 + 27) $ (Substitute $3^x=4$) $ = 4 (36) $ $ = 144 $

📝 Example (6)

Choose the correct answer from the given options:

1 What is the result of $ (a b)^3 \div b^3 $?

a $ a^3 $

b $ \frac{a}{b} $

c $ \frac{a^3}{b^2} $

d $ \frac{a^2}{b^3} $

2 What is the value of $ \frac{(-7)^0}{-(\sqrt{7})^0} $?

a $ 0 $

b $ 6 $

c $ 1 $

d $ -6 $

3 What is the result of $ (\sqrt{3})^3 \times (\sqrt{3})^{-4} $?

a $ \sqrt{3} $

b $ \frac{\sqrt{3}}{3} $

c $ 3 $

d $ \frac{1}{3} $

4 What is the result of $ \sqrt{\frac{5}{10^{-1}}} $?

a $ 5\sqrt{2} $

b $ 5\sqrt{2} $

c $ \frac{5}{\sqrt{10}} $

d $ 2 $

5 What is the perimeter of a square whose area is $ a^4 \text{ cm}^2 $?

a $ a^4 \text{ cm} $

b $ (\sqrt{a})^4 \text{ cm} $

c $ 4\sqrt{a} \text{ cm} $

d $ 4a^2 \text{ cm} $

6 What is the value of $ 4^2 + 4^2 + 4^2 + 4^2 $?

a $ 4^2 $

b $ 4^3 $

c $ 4^8 $

d $ 4^{16} $

7 If $ 2^{x-1} = 1 $, what is the value of $ x $?

a $ 0 $

b $ 1 $

c $ -1 $

d $ -2 $

8 If $ (\sqrt{6})^x \times \sqrt{6}^x = 1 $, what is the value of $ x $?

a $ 0 $

b $ 1 $

c $ -1 $

d $ -2 $

9 What is $ \frac{1}{5} $ of $ (\sqrt{5})^6 $?

a $ 5 $

b $ \sqrt[3]{5} $

c $ (\sqrt{5})^8 $

d $ 25 $

10 If $ 2^x = 3 $, then what is the value of $ 2^{x+1} $?

a $ 4 $

b $ 5 $

c $ 6 $

d $ 9 $

Solution

$ (a b)^3 \div b^3 $ $ = \frac{(ab)^3}{b^3} $ $ = \frac{a^3 b^3}{b^3} $ $ = a^3 $

Correct option: (a) $ a^3 $

$ \frac{(-7)^0}{-(\sqrt{7})^0} $ $ = \frac{1}{-1} $ (Any non-zero number raised to the power of 0 is 1) $ = -1 $

Correct option: (c) $ 1 $

$ (\sqrt{3})^3 \times (\sqrt{3})^{-4} $ $ = (\sqrt{3})^{3 + (-4)} $ $ = (\sqrt{3})^{-1} $ $ = \frac{1}{\sqrt{3}} $ $ = \frac{1}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} $ (Rationalize the denominator) $ = \frac{\sqrt{3}}{3} $

Correct option: (b) $ \frac{\sqrt{3}}{3} $

$ \sqrt{\frac{5}{10^{-1}}} $ $ = \sqrt{5 \times 10^1} $ ($10^{-1} = \frac{1}{10}$, so $\frac{1}{10^{-1}} = 10$) $ = \sqrt{50} $ $ = \sqrt{25 \times 2} $ $ = 5\sqrt{2} $

Correct option: (a) $ 5\sqrt{2} $

Area of square $ = a^4 \text{ cm}^2 $ Side length $ = \sqrt{a^4} = a^2 \text{ cm} $ Perimeter $ = 4 \times \text{side length} $ $ = 4 \times a^2 $ $ = 4a^2 \text{ cm} $

Correct option: (d) $ 4a^2 \text{ cm} $

$ 4^2 + 4^2 + 4^2 + 4^2 $ $ = 4 \times 4^2 $ $ = 4^1 \times 4^2 $ $ = 4^{1+2} $ $ = 4^3 $

Correct option: (b) $ 4^3 $

If $ 2^{x-1} = 1 $ Since $ 2^0 = 1 $, we have $ 2^{x-1} = 2^0 $ Therefore, $ x-1 = 0 $ $ x = 1 $

Correct option: (b) $ 1 $

If $ (\sqrt{6})^x \times \sqrt{6}^x = 1 $ $ (\sqrt{6})^{x+x} = 1 $ $ (\sqrt{6})^{2x} = 1 $ Since $ (\sqrt{6})^0 = 1 $, we have $ (\sqrt{6})^{2x} = (\sqrt{6})^0 $ Therefore, $ 2x = 0 $ $ x = 0 $

Correct option: (a) $ 0 $

What is $ \frac{1}{5} $ of $ (\sqrt{5})^6 $? $ = \frac{1}{5} \times (\sqrt{5})^6 $ $ = 5^{-1} \times (5^{1/2})^6 $ $ = 5^{-1} \times 5^{6/2} $ $ = 5^{-1} \times 5^3 $ $ = 5^{-1+3} $ $ = 5^2 $ $ = 25 $

Correct option: (d) $ 25 $

If $ 2^x = 3 $, then what is the value of $ 2^{x+1} $? $ = 2^x \times 2^1 $ $ = 3 \times 2 $ (Substitute $2^x=3$) $ = 6 $

Correct option: (c) $ 6 $

Lesson: Laws of Exponents in Real Numbers

📖 Learn!

📚 Repeated Multiplication in the Set of Real Numbers

📝 Example (1)

Solution

Zero and Negative Exponents

The Zero Exponent

The Negative Exponent

Important Note

Division by Zero

Laws of Multiplication

Rule 1: Product of Powers with the Same Base

Rule 2: Power of a Product

Important Note: Sum/Difference of Powers

Laws of Division

Rule 1: Quotient of Powers with the Same Base

Rule 2: Power of a Quotient

📝 Example (2)

Solution

📝 Example (3)

Solution

📝 Example (4)

Solution

📝 Example (5)

Solution

📝 Example (6)

Solution

Explore More Math Lessons

Previous: Laws of Square and Cube Roots

Next: Factorization by Extracting the Greatest Common Factor