📚 Learn: Multiplication and Division of Roots
Square Roots
If \(a, b\) are two non-negative real numbers, then:
\(\sqrt{a} \times \sqrt{b} = \sqrt{a \times b}\)
Example: \(\sqrt{2} \times \sqrt{8} = \sqrt{16} = 4\)
\(\frac{\sqrt{a}}{\sqrt{b}} = \sqrt{\frac{a}{b}}\), where \(b \neq 0\)
Example: \(\frac{\sqrt{6}}{\sqrt{2}} = \sqrt{\frac{6}{2}} = \sqrt{3}\)
Cube Roots
If \(a, b\) are two real numbers, then:
\(\sqrt[3]{a} \times \sqrt[3]{b} = \sqrt[3]{a \times b}\)
Example: \(\sqrt[3]{3} \times \sqrt[3]{-4} = \sqrt[3]{-12}\)
\(\frac{\sqrt[3]{a}}{\sqrt[3]{b}} = \sqrt[3]{\frac{a}{b}}\), where \(b \neq 0\)
Example: \(\frac{\sqrt[3]{16}}{\sqrt[3]{2}} = \sqrt[3]{\frac{16}{2}} = \sqrt[3]{8} = 2\)
🔢 Example 1
Put each of the following numbers in the simplest form:
Solution
Analyze the number 32 into two factors, one of which is the largest perfect square (16 × 2).
\(\sqrt{32} = \sqrt{16 \times 2}\)
\(= \sqrt{16} \times \sqrt{2} = 4\sqrt{2}\)
Analyze the number 24 into two factors, one of which is the largest perfect cube (8 × 3).
\(\sqrt[3]{24} = \sqrt[3]{8 \times 3}\)
\(= \sqrt[3]{8} \times \sqrt[3]{3} = 2\sqrt[3]{3}\)
\(2\sqrt{\frac{5}{2}} = 2 \times \frac{\sqrt{5}}{\sqrt{2}}\)
\(= 2 \times \frac{\sqrt{5}}{\sqrt{2}} \times \frac{\sqrt{2}}{\sqrt{2}}\)
\(= 2 \times \frac{\sqrt{10}}{2} = \sqrt{10}\)
\(3\sqrt[3]{\frac{-2}{3}} = 3 \times \frac{\sqrt[3]{-2}}{\sqrt[3]{3}}\)
\(= 3 \times \frac{\sqrt[3]{-2}}{\sqrt[3]{3}} \times \frac{\sqrt[3]{3^2}}{\sqrt[3]{3^2}}\)
\(= 3 \times \frac{\sqrt[3]{-2 \times 9}}{\sqrt[3]{27}} = 3 \times \frac{\sqrt[3]{-18}}{3} = \sqrt[3]{-18}\)
📌 Remember that!
To make the denominator of the irrational number \(\frac{\sqrt[3]{a}}{\sqrt[3]{b}}\) an integer, multiply both its numerator and denominator by \(\sqrt[3]{b^2}\) as follows:
\(\frac{\sqrt[3]{a}}{\sqrt[3]{b}} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}} \times \frac{\sqrt[3]{b^2}}{\sqrt[3]{b^2}} = \frac{\sqrt[3]{ab^2}}{b}\)
To make the denominator of the irrational number \(\frac{\sqrt[3]{a}}{\sqrt[3]{b}}\) an integer, multiply both its numerator and denominator by \(\sqrt[3]{b^2}\) as follows:
\(\frac{\sqrt[3]{a}}{\sqrt[3]{b}} = \frac{\sqrt[3]{a}}{\sqrt[3]{b}} \times \frac{\sqrt[3]{b^2}}{\sqrt[3]{b^2}} = \frac{\sqrt[3]{ab^2}}{b}\)
🔢 Example 2
Simplify each of the following to the simplest form:
Solution
\( 2\sqrt{3} + 5\sqrt{27} - \sqrt{48} \)
\( = 2\sqrt{3} + 5\sqrt{9 \times 3} - \sqrt{16 \times 3} \)
\( = 2\sqrt{3} + 5 \times 3\sqrt{3} - 4\sqrt{3} \)
\( = 2\sqrt{3} + 15\sqrt{3} - 4\sqrt{3} = 13\sqrt{3} \)
\( \frac{\sqrt[3]{40} - 2\sqrt[3]{135}}{\sqrt[3]{5}} \)
\( = \frac{\sqrt[3]{8 \times 5} - 2\sqrt[3]{27 \times 5}}{\sqrt[3]{5}} \)
\( = \frac{\sqrt[3]{8}\sqrt[3]{5} - 2\sqrt[3]{27}\sqrt[3]{5}}{\sqrt[3]{5}} \)
\( = \frac{2\sqrt[3]{5} - 2 \times 3\sqrt[3]{5}}{\sqrt[3]{5}} \)
\( = \frac{2\sqrt[3]{5} - 6\sqrt[3]{5}}{\sqrt[3]{5}} \)
\( = \frac{-4\sqrt[3]{5}}{\sqrt[3]{5}} = -4 \)
Note:
When adding and subtracting unlike radical terms, simplify each term separately. If you get like radical terms, you can add or subtract them.
🔢 Example 3
Geometry: ABC is a triangle whose perimeter is \(\sqrt{1440}\) cm. If \(AB = \sqrt{250}\) cm and \(AC = \sqrt{160}\) cm, find the length of \(\overline{BC}\).
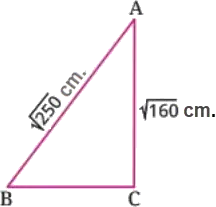
Solution
\( \because \text{Perimeter of the triangle} = \text{Sum of its side lengths} \)
\( \therefore \sqrt{250} + \sqrt{160} + \overline{BC} = \sqrt{1440} \)
\( \therefore \sqrt{25 \times 10} + \sqrt{16 \times 10} + \overline{BC} \)
\( = \sqrt{144 \times 10} \)
\( \therefore 5\sqrt{10} + 4\sqrt{10} + \overline{BC} = 12\sqrt{10} \)
\( \therefore 9\sqrt{10} + \overline{BC} = 12\sqrt{10} \)
\( \therefore \overline{BC} = 12\sqrt{10} - 9\sqrt{10} = 3\sqrt{10} \)
\( \text{i.e., the length of } \overline{BC} \text{ is } 3\sqrt{10} \text{ cm.} \)
🔢 Example 4
If \(x = \sqrt{5} + \sqrt{2}\) and \(y = \frac{3}{x}\), find in the simplest form:
Solution
\( y = \frac{3}{x} = \frac{3}{\sqrt{5} + \sqrt{2}} \times \frac{\sqrt{5} - \sqrt{2}}{\sqrt{5} - \sqrt{2}} \)
\( = \frac{3(\sqrt{5} - \sqrt{2})}{(\sqrt{5})^2 - (\sqrt{2})^2} = \frac{3(\sqrt{5} - \sqrt{2})}{5 - 2} \)
\( = \sqrt{5} - \sqrt{2} \)
\( x - y = (\sqrt{5} + \sqrt{2}) - (\sqrt{5} - \sqrt{2}) \)
\( = \sqrt{5} + \sqrt{2} - \sqrt{5} + \sqrt{2} = 2\sqrt{2} \)
\( \frac{y}{x} = \frac{\sqrt{5} - \sqrt{2}}{\sqrt{5} + \sqrt{2}} \times \frac{\sqrt{5} - \sqrt{2}}{\sqrt{5} - \sqrt{2}} \)
\( = \frac{(\sqrt{5} - \sqrt{2})^2}{5 - 2} = \frac{5 - 2\sqrt{10} + 2}{3} \)
\( = \frac{7 - 2\sqrt{10}}{3} = \frac{7}{3} - \frac{2}{3}\sqrt{10} \)
🤔 Critical Thinking
-
If a, b are two non-negative real numbers:
Is \(\sqrt{a} + \sqrt{b} = \sqrt{a+b}\)?
Let \(a=9, b=16\)
L.H.S \( = \sqrt{9} + \sqrt{16} = 3 + 4 = 7 \)
R.H.S \( = \sqrt{9+16} = \sqrt{25} = 5 \)
\( \because \) L.H.S \( \neq \) R.H.S, the statement is false.
Is \(\sqrt{a} - \sqrt{b} = \sqrt{a-b}\)?
Let \(a=25, b=9\)
L.H.S \( = \sqrt{25} - \sqrt{9} = 5 - 3 = 2 \)
R.H.S \( = \sqrt{25-9} = \sqrt{16} = 4 \)
\( \because \) L.H.S \( \neq \) R.H.S, the statement is false.
-
If a, b are two real numbers:
Is \(\sqrt[3]{a} + \sqrt[3]{b} = \sqrt[3]{a+b}\)?
Let \(a=8, b=27\)
L.H.S \( = \sqrt[3]{8} + \sqrt[3]{27} = 2 + 3 = 5 \)
R.H.S \( = \sqrt[3]{8+27} = \sqrt[3]{35} \)
\( \because \) L.H.S \( \neq \) R.H.S, the statement is false.
Is \(\sqrt[3]{a} - \sqrt[3]{b} = \sqrt[3]{a-b}\)?
Let \(a=64, b=27\)
L.H.S \( = \sqrt[3]{64} - \sqrt[3]{27} = 4 - 3 = 1 \)
R.H.S \( = \sqrt[3]{64-27} = \sqrt[3]{37} \)
\( \because \) L.H.S \( \neq \) R.H.S, the statement is false.
🔢 Example 5
Simplify each of the following to the simplest form:
Solution
\( 2\sqrt{32} - \sqrt{18} + \sqrt{50} \)
\( = 2\sqrt{16 \times 2} - \sqrt{9 \times 2} + \sqrt{25 \times 2} \)
\( = 2 \times 4\sqrt{2} - 3\sqrt{2} + 5\sqrt{2} \)
\( = 8\sqrt{2} - 3\sqrt{2} + 5\sqrt{2} \)
\( = 10\sqrt{2} \)
\( 2\sqrt[3]{16} + \sqrt[3]{54} - \sqrt[3]{128} \)
\( = 2\sqrt[3]{8 \times 2} + \sqrt[3]{27 \times 2} - \sqrt[3]{64 \times 2} \)
\( = 2 \times 2\sqrt[3]{2} + 3\sqrt[3]{2} - 4\sqrt[3]{2} \)
\( = 4\sqrt[3]{2} + 3\sqrt[3]{2} - 4\sqrt[3]{2} \)
\( = 3\sqrt[3]{2} \)
Explore More Math Lessons
You're doing great! Keep learning by exploring these other lessons.
