Lesson 1
Cartesian product
In this lesson, we shall know the concept of the Cartesian product and how to find it and how to represent it graphically.
Before dealing with this subject, we shall remember together what we had studied about the ordered pair.
The ordered pair
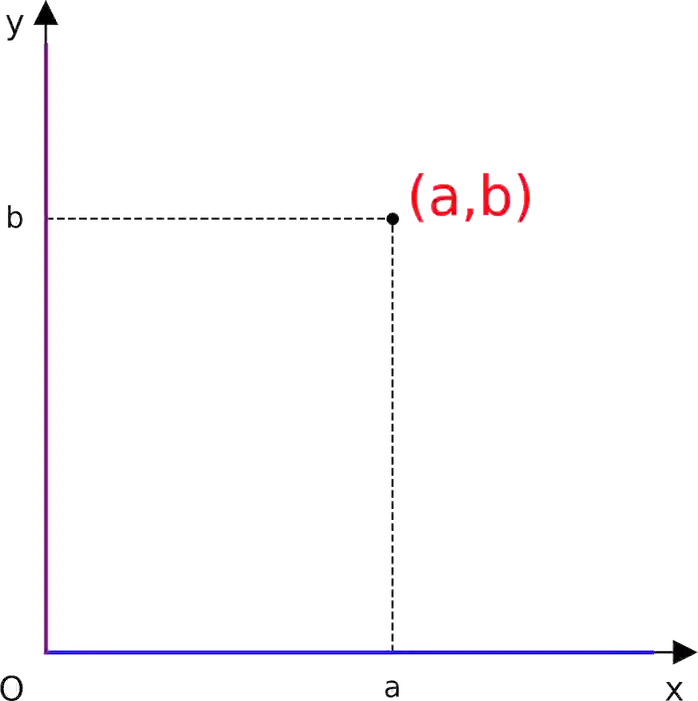
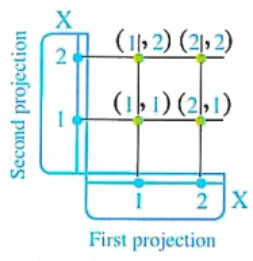
\((a,b)\) is called an ordered pair
- \(a\) is called the first projection
- \(b\) is called the second projection
and the ordered pair \((a,b)\) could be represented by a point as shown in the opposite figure.
! Remarks
-
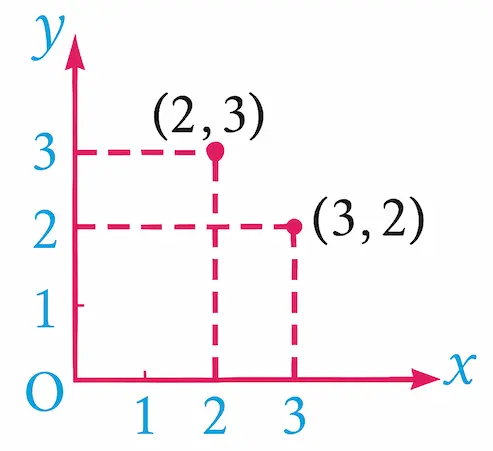
If \(a \neq b\), then \((a,b) \neq (b,a)\).
For example: \((2,3) \neq (3,2)\).and when representing them graphically as shown in the opposite figure, we find that they are represented by two different points.
- The ordered pair is not a set. i.e. \((a,b) \neq \{a,b\}\).
- \((a,a)\) is an ordered pair, while in the sets, we don't write \(\{a,a\}\), but we write \(\{a\}\) without repeating the element a.
- There is an empty set of elements and denoted by the symbol \(\emptyset\), but there is not an empty ordered pair.
The equality of two ordered pairs
If \((a,b) = (x,y)\), then \(a = x\), \(b = y\)
For example:
- If \((a,b) = (3, -4)\), then \(a = 3\), \(b = -4\)
- If \((x,2) = (-5, y)\), then \(x = -5\), \(y = 2\)
Example 1
Choose the correct answer from the given ones :
1. If \((3, 8) = (3, \sqrt[3]{y})\), then \(\sqrt[3]{y}\) = ..........
2. If \((32, x+y) = (y^5, 2)\), then \(x\) = ..........
3. If \((2^{x-1}, -3) = (1, y)\), then \(2x-y\) = ..........
4. If \((x^2-1, 4) = (48, 2y)\), then \(xy\) = ..........
Solution
1 (b) The reason : \(\because (3, 8) = (3, \sqrt[3]{y})\)
\(\therefore \sqrt[3]{y} = 8\)
\(\therefore y = 8^2\)
\(\therefore y = 64\)
\(\therefore \sqrt[3]{y} = \sqrt[3]{64}\)
\(\therefore \sqrt[3]{y} = 4\)
2 (a) The reason : \(\because (32, x+y) = (y^5, 2)\)
\(\therefore y^5 = 32\)
\(\therefore y=2\) «because \(2^5 = 32\)»
, \(x+y=2\)
substituting by \(y=2\)
\(\therefore x+2=2\)
\(\therefore x=0\)
3 (d) The reason : \(\because (2^{x-1}, -3) = (1, y)\)
\(\therefore y = -3\)
, \(2^{x-1} = 1\)
then \(x-1=0\)
\(\therefore x=1\)
\(\therefore 2x-y = 2 \times 1 - (-3)\)
\(= 2+3\)
\(= 5\)
4 (d) The reason : \(\because (x^2-1, 4) = (48, 2y)\)
\(\therefore x^2-1=48\)
\(\therefore x^2 = 49\)
\(\therefore x = \pm\sqrt{49}\)
\(\therefore x = \pm 7\)
, \(2y=4\)
\(\therefore y = \frac{4}{2}\)
\(\therefore y = 2\)
\(\therefore xy = \pm 7 \times 2\)
\(\therefore xy = \pm 14\)
The Cartesian product of two finite sets
For any two finite and non empty sets \(X\) and \(Y\), we get :
The Cartesian product of the set \(X\) by the set \(Y\) and it is denoted by \(X \times Y\) is the set of all ordered pairs whose first projection of each of them belongs to \(X\) and the second projection of each of them belongs to \(Y\).
i.e. \(X \times Y = \{(a,b) : a \in X, b \in Y\}\)
For example :
1 If \(X = \{1, 2\}\) , \(Y = \{5, 7, 8\}\) , then :
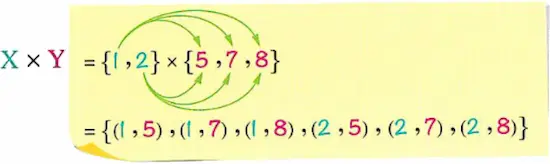
We can represent \(X \times Y\) by two ways as follows :
1st way : The arrow diagram
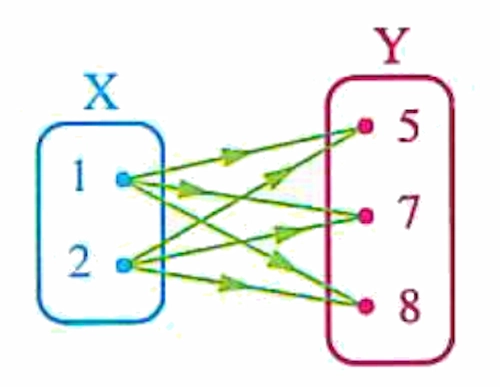
In this method, an arrow is drawn from each element of the first set (X), which represents the first projection, to every element of the second set (Y), which represents the second projection. This visually maps all possible ordered pairs.
2nd way : The graphical (Cartesian) diagram
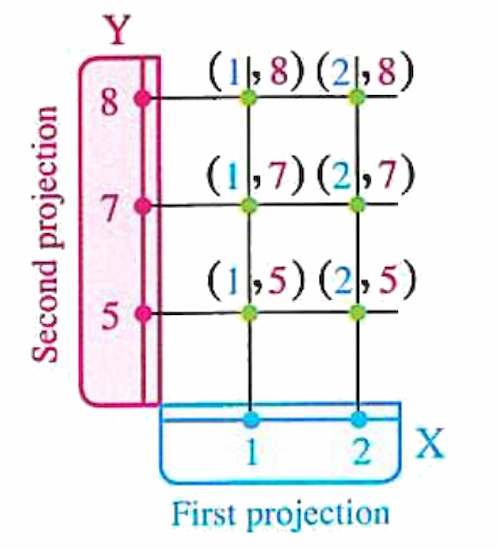
Here, the elements of set X are represented on the horizontal axis, and the elements of set Y are on the vertical axis. The points where the horizontal and vertical lines intersect represent the ordered pairs of the Cartesian product \(X \times Y\).
2 If \(X = \{1, 2\}\) , \(Y = \{5, 7, 8\}\) , then :

Similarly, the Cartesian product \(Y \times X\) can also be represented in the following two ways:
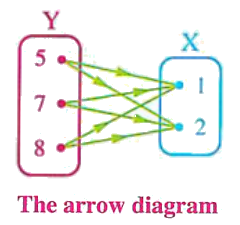
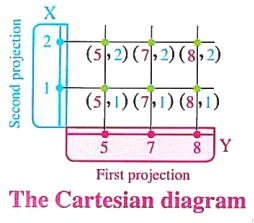
The Cartesian product of a set by itself
The Cartesian product of a set \(X\) with itself is denoted by \(X \times X\) or \(X^2\) (read as "X two"). It is defined as the set of all ordered pairs where both the first and second elements (projections) belong to the set \(X\).
i.e. \(X \times X = \{(a,b) : a \in X, b \in X\}\)
For example:
If \(X = \{1, 2\}\) , then :

The Cartesian product \(X \times X\) can be visualized using two methods:
1 The arrow diagram
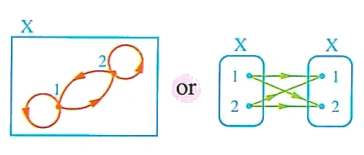
Notice that: The circular arrow starting from a point and returning to it is called a "loop". This is used to show that an element is paired with itself, representing pairs like (1, 1) or (2, 2).
2 The Cartesian diagram
Example 2
If \(X = \{2, 3, 4\}\) and \(Y = \{a, b\}\), find each of :
Solution
1. \(X \times Y = \{(2, a), (2, b), (3, a), (3, b), (4, a), (4, b)\}\)
2. \(Y \times X = \{(a, 2), (a, 3), (a, 4), (b, 2), (b, 3), (b, 4)\}\)
\(X \times X = \{(2, 2), (2, 3), (2, 4), (3, 2), (3, 3), (3, 4), (4, 2), (4, 3), (4, 4)\}\)
4. \(Y^2 = \{(a, a), (a, b), (b, a), (b, b)\}\)
The number of the elements of the Cartesian product
If we denote the number of elements of the set \(X\) by \(n(X)\) and the number of elements of the set \(Y\) by \(n(Y)\), then the number of elements of the Cartesian product \(X \times Y\) is denoted by \(n(X \times Y)\), and:
- \(n(X \times Y) = n(Y \times X) = n(X) \times n(Y)\)
- \(n(X \times X) = n(X) \times n(X) = [n(X)]^2\)
- \(n(X \times \emptyset) = n(X) \times n(\emptyset) = 0\) [Because \(n(\emptyset) = 0\)]
Notice that: If \(X\) and \(Y\) are two finite and non-empty sets where \(X \neq Y\), then \(X \times Y \neq Y \times X\), but the number of elements is the same, so \(n(X \times Y) = n(Y \times X)\).
For example :
If \(X = \{2, -1, 0\}\) and \(Y = \{5, -7\}\), then \(n(X) = 3\), \(n(Y) = 2\), then :
\(n(X \times Y) = 3 \times 2 = 6\)
\(n(Y \times X) = 2 \times 3 = 6\)
\(n(X^2) = 3^2 = 9\)
\(n(Y^2) = 2^2 = 4\)
Find the previous Cartesian products and verify the number of their elements.
Example 3
Choose the correct answer from the given ones :
1. If \(X = \{0, 2\}\) , \(n(Y) = 5\), then \(n(X \times Y)\) = ..........
2. If \(n(Y) = 4\) , \(n(X \times Y) = 8\), then \(n(X)\) = ..........
3. If \(n(X^2) = 9\) , \(n(Y^2) = 16\), then \(n(Y \times X)\) = ..........
Solution
1 (d) The reason : \(\because n(X) = 2\), \(n(Y) = 5\)
\(\therefore n(X \times Y) = 2 \times 5\)
\(= 10\)
2 (a) The reason :
\(n(X) = \frac{n(X \times Y)}{n(Y)}\)
\(= \frac{8}{4}\)
\(= 2\)
3 (b) The reason :
\(\because n(X^2) = 9 \implies \therefore n(X) = \sqrt{9} = 3\)
\(\because n(Y^2) = 16 \implies \therefore n(Y) = \sqrt{16} = 4\)
\(\therefore n(Y \times X) = 4 \times 3\)
\(= 12\)
Example 4
If \(X = \{a, b\}\) , \(Y = \{3, 5, 7\}\) , \(Z = \{5, 7, 9\}\), represent the sets X, Y and Z by a Venn diagram, then find:
- \(X \times (Y \cup Z)\) , \((X \times Y) \cup (X \times Z)\)
- \(X \times (Y \cap Z)\) , \((X \times Y) \cap (X \times Z)\)
- \(X \times (Z - Y)\) , \((X \times Z) - (X \times Y)\)
Solution
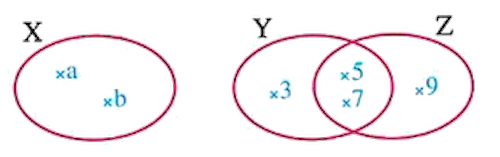
1.
\(\because Y \cup Z = \{3, 5, 7, 9\}\)
\(\therefore X \times (Y \cup Z) = \{a, b\} \times \{3, 5, 7, 9\}\)
\(= \{(a, 3), (a, 5), (a, 7), (a, 9), (b, 3), (b, 5), (b, 7), (b, 9)\}\)
\(\because X \times Y = \{a, b\} \times \{3, 5, 7\}\)
\(= \{(a, 3), (a, 5), (a, 7), (b, 3), (b, 5), (b, 7)\}\) ... (1)
\(\because X \times Z = \{a, b\} \times \{5, 7, 9\}\)
\(= \{(a, 5), (a, 7), (a, 9), (b, 5), (b, 7), (b, 9)\}\) ... (2)
From (1) and (2):
\(\therefore (X \times Y) \cup (X \times Z) = \)
\(\{(a, 3), (a, 5), (a, 7), (a, 9), (b, 3), (b, 5), (b, 7), (b, 9)\}\)
2.
\(\because Y \cap Z = \{5, 7\}\)
\(\therefore X \times (Y \cap Z) = \{a, b\} \times \{5, 7\}\)
\(= \{(a, 5), (a, 7), (b, 5), (b, 7)\}\)
From (1) and (2):
\(\therefore (X \times Y) \cap (X \times Z) = \{(a, 5), (a, 7), (b, 5), (b, 7)\}\)
3.
\(\because Z - Y = \{9\}\)
\(\therefore X \times (Z - Y) = \{a, b\} \times \{9\}\)
\(= \{(a, 9), (b, 9)\}\)
From (1) and (2):
\(\therefore (X \times Z) - (X \times Y) = \{(a, 9), (b, 9)\}\)
Representing the Cartesian product ℝ × ℝ (ℝ²)
The Cartesian product \(ℝ \times ℝ\), also denoted as \(ℝ^2\), is represented by a perpendicular graphical grid. This grid forms an infinite surface that extends in all directions. The figure shown illustrates just a small portion of this vast region.
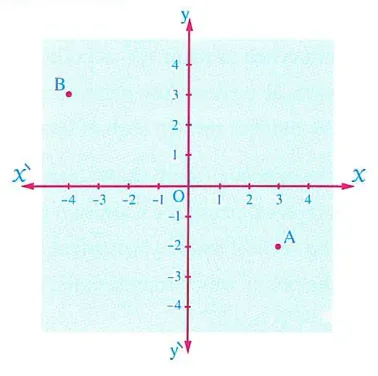
Every single point within this graphical grid corresponds to a unique ordered pair in the Cartesian product \(ℝ \times ℝ\).
For example:
- The point A represents the ordered pair \((3, -2)\).
- The point B represents the ordered pair \((-4, 3)\).
Remarks
- The horizontal line \(\overleftrightarrow{XX'}\) is the X-axis, and the vertical line \(\overleftrightarrow{yy'}\) is the Y-axis.
- The intersection of these two axes is known as the origin point.
- For any point A representing an ordered pair \((x, y)\) in the Cartesian product \(ℝ \times ℝ\):
- The first projection, \(x\), is the X-coordinate of point A.
- The second projection, \(y\), is the Y-coordinate of point A.
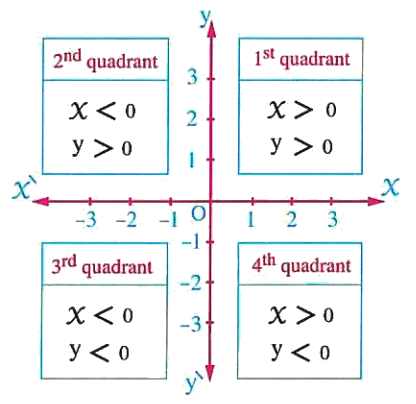
- The axes \(\overleftrightarrow{XX'}\) and \(\overleftrightarrow{yy'}\) divide the plane into four quadrants. The quadrant of any point can be determined by the signs of its coordinates.
- If the X-coordinate of a point is 0, the point lies on the Y-axis.
- If the Y-coordinate of a point is 0, the point lies on the X-axis.
Example 5
Choose the correct answer from the given ones :
1. The point \((4, -3)\) lies on the .......... quadrant.
2. Which of the following points lies on the third quadrant?
3. If the point \((a, 3-a)\) lies on the X-axis, then \(a\) = ..........
4. If \(b < 2\), then the point \((b-2, 4)\) lies on the .......... quadrant.
5. If the point \((X-3, 4-X)\) where \(X \in ℤ\) lies on the fourth quadrant, then \(X\) = ..........
Solution
1 (d) The reason : Because the X-coordinate is positive and the y-coordinate is negative.
2 (d) The reason : Because the X-coordinate and the y-coordinate of all the points on the third quadrant are negative.
3 (c) The reason : \(\because (a, 3-a) \in \overleftrightarrow{XX'}\)
\(\therefore 3-a=0\)
\(\therefore a=3\)
4 (b) The reason : \(\because b < 2\)
\(\therefore\) The X-coordinate of the point \((b-2, 4)\) is negative and its y-coordinate is positive.
\(\therefore (b-2, 4)\) lies on the second quadrant.
5 (d) The reason : Because at \(X=5\), then \((X-3, 4-X) = (2, -1)\)
i.e. The X-coordinate is positive and the y-coordinate is negative.