What are intervals in mathematics for Prep 2?

An interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For Prep 2 students in the Egyptian curriculum, this concept is crucial for understanding subsets of real numbers and is represented using brackets [] for closed intervals and parentheses () for open intervals.

How do you represent intervals on a number line?

Intervals are represented on a number line by shading the portion of the line that corresponds to the numbers in the interval. A closed circle (●) is used at the endpoint if the number is included in the interval (using ≤ or ≥), and an open circle (○) is used if the endpoint is not included (using ).

What are the main operations on intervals?

The main operations on intervals are: 1. Union (∪): Combining all elements from two intervals. 2. Intersection (∩): Finding the common elements between two intervals. 3. Difference (-): Finding elements in the first interval that are not in the second. 4. Complement ('): Finding all real numbers that are not in the interval.

ما هي الفترات في الرياضيات للصف الثاني الإعدادي؟

الفترة هي مجموعة من الأعداد الحقيقية التي تحتوي على جميع الأعداد الواقعة بين أي عددين في المجموعة. بالنسبة لطلاب الصف الثاني الإعدادي في المنهج المصري، هذا المفهوم أساسي لفهم المجموعات الجزئية من الأعداد الحقيقية ويتم تمثيلها باستخدام الأقواس [] للفترات المغلقة والأقواس () للفترات المفتوحة.

كيف يتم تمثيل الفترات على خط الأعداد؟

يتم تمثيل الفترات على خط الأعداد بتظليل الجزء من الخط الذي يتوافق مع الأعداد في الفترة. تُستخدم دائرة مغلقة (●) عند نقطة النهاية إذا كان العدد ضمن الفترة (باستخدام ≤ أو ≥)، ودائرة مفتوحة (○) إذا لم تكن نقطة النهاية ضمن الفترة (باستخدام ).

ما هي العمليات الرئيسية على الفترات؟

العمليات الرئيسية على الفترات هي: ١. الاتحاد (∪): دمج جميع العناصر من فترتين. ٢. التقاطع (∩): إيجاد العناصر المشتركة بين فترتين. ٣. الفرق (-): إيجاد العناصر الموجودة في الفترة الأولى وغير موجودة في الثانية. ٤. المكملة ('): إيجاد جميع الأعداد الحقيقية غير الموجودة في الفترة.

Intervals and Their Operations | Math Egypt - Mr. Ayman Hassan مستر أيمن حسن

🧠 Think and Discuss!

One day, Mustafa's lecture schedule at the university was as follows:

🕒 From 9:00 AM to 12:00 PM.
🕒 Then from 2:00 PM to 4:00 PM.

If the university's sports center 🏋️ is open daily from 10:00 AM to 1:00 PM, what is the suitable time interval for Mustafa to practice sports at the university's sports center on this day without it affecting his lecture attendance? Discuss.

An illustration of time intervals for a student's schedule by Math Egypt - Mr. Ayman Hassan (رسم توضيحي للفترات الزمنية لجدول طالب من ماث إيجيبت - مستر أيمن حسن)

✅ Solution

Here is a step-by-step solution to find the suitable time for Mustafa to go to the sports center:

Identify Mustafa's Busy Times (Lectures):
- 🕒 Lecture 1: The interval [9:00 AM, 12:00 PM]
- 🕒 Lecture 2: The interval [2:00 PM, 4:00 PM]
Identify the Sports Center's Open Hours:
🏋️ The center is open during the interval [10:00 AM, 1:00 PM].
Find the Overlap:
We need to find a time when the sports center is open AND Mustafa is free.

Let's compare the sports center's open hours with Mustafa's lecture times.
- 🕒 The first lecture (9:00 AM - 12:00 PM) overlaps with the center's hours (10:00 AM - 1:00 PM). The specific time of conflict is from 10:00 AM to 12:00 PM. During this period, Mustafa is in a lecture, so he cannot go to the gym.
- 🕒 The second lecture (2:00 PM - 4:00 PM) does not overlap with the center's hours, as the center closes at 1:00 PM.
Determine the Available Time Slot:
- 🏋️ The center is open from 10:00 AM to 1:00 PM.
- 🕒 Mustafa is busy from 10:00 AM until 12:00 PM.
- This leaves the period when the center is still open after his lecture ends.
Conclusion:
✅ The only time Mustafa can go to the sports center is after his first lecture ends at 12:00 PM and before the center closes at 1:00 PM.

Therefore, the suitable time interval for Mustafa is from 12:00 PM to 1:00 PM.

📖 Learn!

📚 Intervals

Between any two real numbers, there is an infinite number of real numbers.

The set of real numbers and its subsets cannot be expressed by the listing method because it is impossible to list all their elements. Therefore, another method is used to express them, which is "intervals".

❓ Example (1)

Problem 1

Write in interval notation, then represent the set A on the number line:

\(A = \{x : x \in \mathbb{R}, 1 \le x \le 3\}\)

Does \(\sqrt{2} \in A\)?

Problem 2

Write in interval notation, then represent the set B on the number line:

\(B = \{x : x \in \mathbb{R}, -2 < x < 2\}\)

Does \(\sqrt[3]{-9} \in B\)?

Solution

Solution ①

\(A = [1, 3]\)

Number line for the closed interval [1, 3] by Math Egypt - Mr. Ayman Hassan (خط الأعداد للفترة المغلقة [١، ٣] من ماث إيجيبت - مستر أيمن حسن)

Using a calculator:

\(\sqrt{2} \approx 1.4\)

\(\because 1 \le 1.4 \le 3\)

\(\therefore \sqrt{2} \in [1, 3]\)

Solution ②

\(B = \mathopen{]} -2, 2 \mathclose{[}\)

Number line for the open interval ]-2, 2[ by Math Egypt - Mr. Ayman Hassan (خط الأعداد للفترة المفتوحة ]-٢، ٢[ من ماث إيجيبت - مستر أيمن حسن)

Using a calculator:

\(\sqrt[3]{-9} \approx -2.08\)

\(\because \sqrt[3]{-9} < -2\)

\(\therefore \sqrt[3]{-9} \notin \mathopen{]} -2, 2 \mathclose{[}\)

♾️ Unbounded Intervals

The set of real numbers extends on the number line in the positive direction to infinity \((\infty)\) and extends in the negative direction to negative infinity \((-\infty)\).
The symbols \(\infty\) and \(-\infty\) are used to express unbounded sets as follows:
If \(a \in \mathbb{R}\), then:

The set of real numbers greater than or equal to \(a\)

\([a, \infty[\) = \(\{x : x \in \mathbb{R}, x \ge a\}\)

Number line for the unbounded interval [a, infinity) by Math Egypt - Mr. Ayman Hassan (خط الأعداد للفترة غير المحدودة [أ، ∞) من ماث إيجيبت - مستر أيمن حسن)

The set of real numbers less than or equal to \(a\)

\(]-\infty, a]\) = \(\{x : x \in \mathbb{R}, x \le a\}\)

Number line for the unbounded interval (-infinity, a] by Math Egypt - Mr. Ayman Hassan (خط الأعداد للفترة غير المحدودة (-∞، أ] من ماث إيجيبت - مستر أيمن حسن)

The set of real numbers greater than \(a\)

\(]a, \infty[\) = \(\{x : x \in \mathbb{R}, x > a\}\)

The set of real numbers less than \(a\)

\(]-\infty, a[\) = \(\{x : x \in \mathbb{R}, x < a\}\)

Note that:

The interval \(]-\infty, \infty[\) represents the set of real numbers \(\mathbb{R}\), and \(\infty \notin \mathbb{R}\) and \(-\infty \notin \mathbb{R}\).

📝 Example (2)

Write each of the following sets in interval notation and represent it on the number line:

1. The set of positive real numbers.

2. The set of non-positive real numbers.

3. \( \{x : x \in \mathbb{R}, x \ge -2\} \)

4. \( \{x : x \in \mathbb{R}, x < 1\} \)

Solution

Solution ①

\([0, \infty[\)

Number line for the set of non-negative real numbers [0, infinity) by Math Egypt - Mr. Ayman Hassan (خط الأعداد لمجموعة الأعداد الحقيقية غير السالبة [٠، ∞) من ماث إيجيبت - مستر أيمن حسن)

Solution ②

\( ]-\infty, 0] \)

Number line for the set of non-positive real numbers (-infinity, 0] by Math Egypt - Mr. Ayman Hassan (خط الأعداد لمجموعة الأعداد الحقيقية غير الموجبة (-∞، ٠] من ماث إيجيبت - مستر أيمن حسن)

Solution ③

\([-2, \infty[\)

Number line for the interval [-2, infinity) by Math Egypt - Mr. Ayman Hassan (خط الأعداد للفترة [-٢، ∞) من ماث إيجيبت - مستر أيمن حسن)

Solution ④

\( ]-\infty, 1[\)

Number line for the interval (-infinity, 1) by Math Egypt - Mr. Ayman Hassan (خط الأعداد للفترة (-∞، ١) من ماث إيجيبت - مستر أيمن حسن)

📘 Notes on Real Number Sets

Note that:

•
\( \mathbb{R} = \mathbb{R}^+ \cup \{0\} \cup \mathbb{R}^- \)
Where:
\(\mathbb{R}^+\) is the set of positive real numbers.
\(\mathbb{R}^-\) is the set of negative real numbers.
•
The set of non-negative real numbers = \( \mathbb{R}^+ \cup \{0\} \)
•
The set of non-positive real numbers = \( \mathbb{R}^- \cup \{0\} \)

📐 Operations on Intervals

Using the number line, find each of the following:

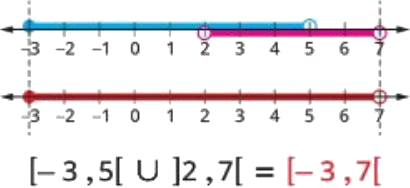
1. \( [-3, 5] \cup [2, 7[ \)
2. \( \mathopen{]}1, 5] \cap \mathopen{]}-\infty, 3] \)
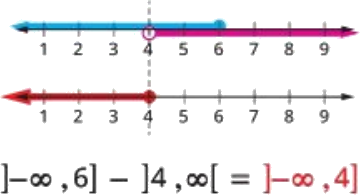
3. \( \mathopen{]}-\infty, 6] - \mathopen{]}4, \infty[ \)
4. \( \mathopen{]}-\infty, 3[' \)

Solution

Solution (1)

Number line for the union of two intervals by Math Egypt - Mr. Ayman Hassan (خط الأعداد لاتحاد فترتين من ماث إيجيبت - مستر أيمن حسن)

\( = [-3, 7[ \)

Solution (2)

Number line for the intersection of two intervals by Math Egypt - Mr. Ayman Hassan (خط الأعداد لتقاطع فترتين من ماث إيجيبت - مستر أيمن حسن)

\( = \mathopen{]}1, 3] \)

Solution (3)

Number line for the difference between two intervals by Math Egypt - Mr. Ayman Hassan (خط الأعداد للفرق بين فترتين من ماث إيجيبت - مستر أيمن حسن)

\( = \mathopen{]}-\infty, 4] \)

Solution (4)

Number line for the complement of an interval by Math Egypt - Mr. Ayman Hassan (خط الأعداد لمكملة فترة من ماث إيجيبت - مستر أيمن حسن)

\( = [3, \infty[ \)

⭐ Example (4): Choose the Correct Answer

1. \(4 \in \text{...........}\)

a\( [4, 7[ \)

b\( [-4, 4] \)

c\( ]2, 5[ \)

d\( ]-11, -4] \)

Correct Answer: (c). The number 4 is greater than 2 and less than 5.

2. \(\sqrt[3]{-8} \text{...........} [-8, -2[\)

a\( \in \)

b\( \notin \)

c\( \subset \)

d\( \not\subset \)

Correct Answer: (b). Because \(\sqrt[3]{-8} = -2\), and the interval \( [-8, -2[ \) is open at -2, which means -2 is not included in the interval.

3. \(\{1, 6\} \text{...........} ]1, 6]\)

a\( \in \)

b\( \notin \)

c\( \subset \)

d\( \not\subset \)

Correct Answer: (d). For a set to be a subset, all its elements must belong to the other set. Here, \(1 \notin ]1, 6]\) because the interval is open at 1.

4. If \(x \in [-5, \infty[\), then ...........

a\( x > -5 \)

b\( x \ge -5 \)

c\( x < -5 \)

d\( x \le -5 \)

Correct Answer: (b). The interval \( [-5, \infty[ \) includes all real numbers greater than or equal to -5.

5. The sum of the real numbers in the interval \( [-3, 3[ \) is ...........

a-6

b-3

czero

Correct Answer: (b). For every number \(x\) in the interval \( (0, 3) \), its additive inverse \(-x\) is also in the interval \( [-3, 0) \). These pairs sum to zero. The number 0 is also in the interval. The only number remaining that does not have its additive inverse within the interval is -3. Therefore, the conceptual sum is -3.

📝 Example (5): Operations on Intervals

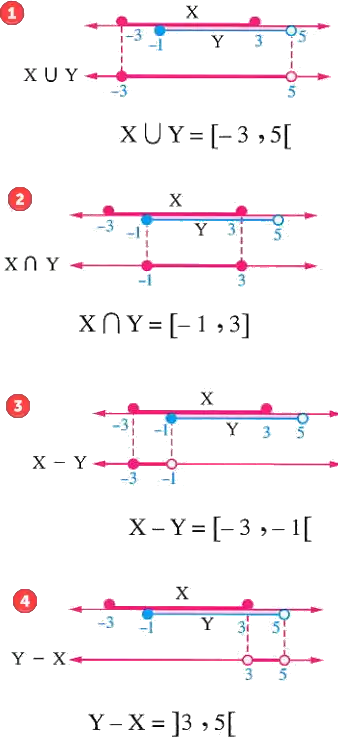
If \(X = [-3, 3]\) and \(Y = [-1, 5[\), find using the number line:

1 \( X \cup Y \)

2 \( X \cap Y \)

3 \( X - Y \)

4 \( Y - X \)

Solution

Explore More Math Lessons

You're doing great! Keep learning by exploring these other lessons.

Previous: The Set of Real Numbers (R)

Go back and review the basics of rational and irrational numbers.

Next: Operations on Real Numbers

Learn about operations like addition, subtraction, multiplication, and division of real numbers.