Lesson 2: Applications of Ratio and Proportion
First: Scale Drawings
Ahmed took a picture of his brother, and his brother's height in the picture was 5 cm, knowing that his brother's real height is 120 cm.
And this means
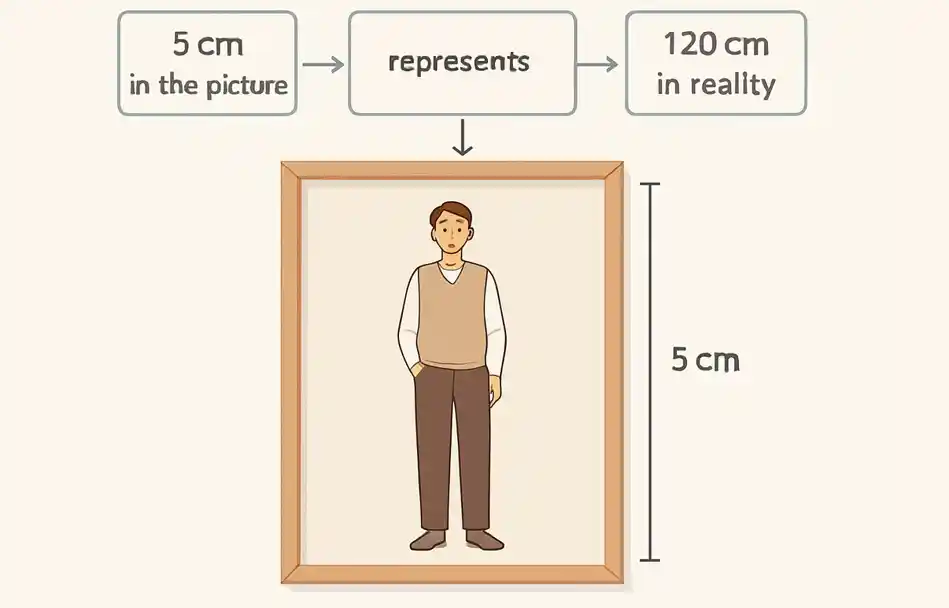
To clarify this concept, the ratio between his brother's height in the drawing and his real height can be represented as:
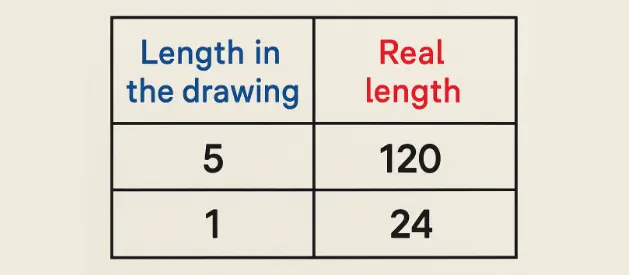
This means that every 1 cm in the picture represents 24 cm in reality.
Concept of Scale Drawings
Scale Drawings: It is a ratio of the dimension in the drawing or model to the dimension in reality.
Scale of Drawing = \(\frac{\text{The length in the drawing}}{\text{The real length}}\)
Example 1
A) If the distance between two cities is 80 km and the distance between them on a map is 4 cm, find the scale drawing for this map.
B) An enlarged picture of an insect, its real length is 0.5 mm and its length in the picture is 7.5 cm, find the scale drawing.
Solution
A) The scale drawing = \(\frac{\text{The length in the drawing}}{\text{The real length}}\)
= \(\frac{4 \text{ cm}}{80 \text{ km}}\)
= \(\frac{4}{8,000,000} = \frac{1}{2,000,000}\)
The scale drawing can be written as 1 : 2,000,000
Note
In Example 1, the scale drawing 1 : 2,000,000, means every 1 cm in the drawing represents 20 km in reality.
Remember
1 Kilometer = 1,000 Meters
1 Meter = 100 cm
So 1 kilometer = 100,000 cm
B) The length in the drawing : The real length
7.5 cm : 0.5 mm
(Note: 7.5 cm = 7.5 x 10 = 75 mm)
75 mm : 0.5 mm (Multiply by 10)
750 : 5 (Divide by 5)
150 : 1
The scale drawing is 150 : 1.
Notice that:
In Example B, the scale drawing 150 : 1, means that every 15 cm in the drawing represent 1 mm in reality.
.webp)
Example 2
In each of the following, find the scale drawing and determine whether it is for magnification or minimization:
A) The distance between two cities on the map is 3.2 cm, and the real distance between them is 64 km.
B) A picture of a butterfly, where its real length is 2.5 cm and its length in the picture is 2 meters.
Solution
A) The scale drawing = \(\frac{\text{The length in the drawing}}{\text{The real length}}\)
= \(\frac{3.2 \text{ cm}}{64 \text{ km}}\)
= \(\frac{3.2}{6,400,000}\)
= \(\frac{32}{64,000,000} = \frac{1}{2,000,000}\)
The scale drawing is 1 : 2,000,000. Since the scale is less than 1, it is a minimization.
B) The length in the drawing : The real length
2 meters : 2.5 cm
(Note: 2 meters = 2 x 100 = 200 cm)
200 cm : 2.5 cm (Multiply by 10)
2000 : 25 (Divide by 25)
80 : 1
The scale drawing is 80 : 1. Since the scale is greater than 1, it is a magnification.
Example 3
How to Find the Real Length or the Drawing Length
If the scale drawing on a map is 1 : 500,000 and the distance between two cities on the map is 3 cm, find the real distance between the two cities.
Solution
The scale drawing = \(\frac{\text{The distance on the map}}{\text{The real distance}}\)
\(\frac{1}{500,000} = \frac{3 \text{ cm}}{\text{The real distance}}\)
The real distance = \(\frac{3 \text{ cm} \times 500,000}{1}\)
Example 4
If the distance between two cities on the map is 2.5 cm, find the real distance between the two cities. If the scale drawing of the map is 1:4,000,000
Solution
The scale drawing = \(\frac{\text{The distance on the map}}{\text{The real distance}}\)
\(\frac{1}{4,000,000} = \frac{2.5 \text{ cm}}{\text{The real distance}}\)
The real distance = \(2.5 \text{ cm} \times 4,000,000\)
Example 5
If the distance between two cities is 24 km, then find the distance in cm between the two cities on a map given that the scale drawing of the map is 1 : 400,000
Solution
The scale drawing = \(\frac{\text{The distance on the map}}{\text{The real distance}}\)
\(\frac{1}{400,000} = \frac{\text{The distance on the map}}{(24 \times 100,000) \text{ cm}}\)
The distance on the map = \(\frac{(24 \times 100,000) \text{ cm} \times 1}{400,000} = 6 \text{ cm}\)
Example 6
If the distance between two cities is 26 km, then find the distance in cm between the two cities on a map given that the scale drawing of the map is 1 : 650,000
Solution
The scale drawing = \(\frac{\text{The distance on the map}}{\text{The real distance}}\)
\(\frac{1}{650,000} = \frac{\text{The distance on the map}}{(26 \times 100,000) \text{ cm}}\)
The distance on the map = \(\frac{(26 \times 100,000) \text{ cm} \times 1}{650,000} = 4 \text{ cm}\)
Note
The scale drawings on maps can be expressed as follows:

This means that every 1 cm on the map represents 20 km in reality.
Example 7
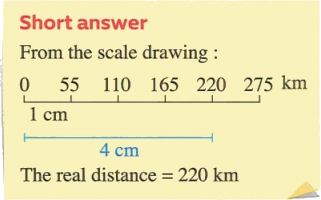
Use the ruler to measure the distance between Cairo and Alexandria on the opposite map, and use the map scale to find the actual distance between Cairo and Alexandria.
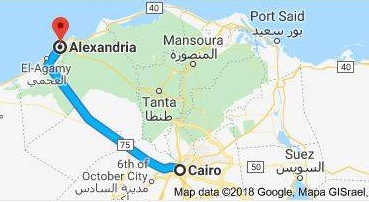
Solution
Use a ruler to find the distance between the two governorates on the map, which is approximately 4 cm, and since every 1 cm on the map represents 55 km in reality.
The scale drawing = \(\frac{\text{The distance on the map}}{\text{The real distance}}\)
\(\frac{1 \text{ cm}}{55 \text{ km}} = \frac{4 \text{ cm}}{\text{The real distance}}\)
i.e. The real distance = \(\frac{4 \times 55}{1}\)
= 220 km