Lesson 1: Ratio and Proportion
Part 1: Ratio
A ratio is a method of comparing two quantities of the same kind. It expresses the relationship between a part and a part, a part and a whole, or a whole and a part.
You can express the ratio between a and b in each of the following forms:
\(\frac{a}{b}\) \(a : b\) a to b
Where a and b are terms of the ratio.
Example 1 (Ratio)
A choir consists of 15 pupils, 7 boys and the rest are girls. In each of the following, write the ratio between:
- The number of boys to the total number in the choir.
- The number of girls to the number of boys.
- The total number in the choir to the number of girls.
Solution
- The ratio between the number of boys and the total number in the choir is \(7 : 15\) (or \(\frac{7}{15}\)). «part to whole»
- The ratio between the number of girls and the number of boys is \(8 : 7\) (or \(\frac{8}{7}\)). «part to part»
- The ratio between the total number in the choir and the number of girls is \(15 : 8\) (or \(\frac{15}{8}\)). «whole to part»
Equivalent Ratios
You can find a ratio equivalent to a given ratio by multiplying or dividing both terms of the ratio by the same number (except zero).
Example 2 (Ratio)
Solution
Multiply: \(\frac{16 \times 2}{24 \times 2} = \frac{32}{48}\)
Divide: \(\frac{16 \div 8}{24 \div 8} = \frac{2}{3}\)
Solution
Since \(3 \times 2 = 6\), we multiply the denominator by 2 as well: \(X = 4 \times 2 = 8\)
Writing the Ratio in Simplest Form
You can write the ratio in its simplest form by dividing both terms by their greatest common factor, or by dividing both terms by the same factor until they have no common factor except one.
Example 3 (Ratio)
Write the simplest form of the ratio 30 : 20
Solution
Divide both terms by the GCF, 10.
\(30 : 20 \xrightarrow{\div 10} 3 : 2\)
Another Solution
Divide by common factors.
\(30 : 20 \xrightarrow{\div 2} 15 : 10 \xrightarrow{\div 5} 3 : 2\)
Rate
It is a ratio that compares two quantities with different units of measurement.
Example: 180 kilometers in 3 hours.
• When simplifying a rate till it has a denominator of 1, it is called a unit rate.
Example: \(\frac{180 \text{ km}}{3 \text{ hours}} \xrightarrow{\div 3} \frac{60 \text{ km}}{1 \text{ hour}}\) (unit rate)
Part 2: Proportion
Concept of Proportion
A proportion is an equality of at least two ratios or two rates.
Example: \(\frac{4}{8} = \frac{1}{2}\) or \(\frac{8 \text{ eggs}}{2 \text{ cups}} = \frac{4 \text{ eggs}}{1 \text{ cup}}\)
Writing Proportion
• If a, b, c, d are proportional quantities, then: \(\frac{a}{b} = \frac{c}{d}\)
Ex: 3, 4, 6, 8 are proportional, so \(\frac{3}{4} = \frac{6}{8}\)
• Vice versa, if \(\frac{a}{b} = \frac{c}{d}\), then a, b, c, d are proportional.
'a' & 'd' are Extremes
'b' & 'c' are Means
Property of Cross Multiplication
If two ratios are equal: Product of Extremes = Product of Means
• If \(\frac{a}{b} = \frac{c}{d}\), then \(a \times d = b \times c\)
Ex: \(\frac{3}{4} = \frac{6}{8} \implies 3 \times 8 = 4 \times 6 \implies 24 = 24\)
Example 1 (Proportion)
Determine which pair represents a proportion:
Solution
\(1 \times 10 = 10\) (Extremes)
\(8 \times 6 = 48\) (Means)
\(10 \neq 48\), so it's not a proportion.
\(8 \times 15 = 120\) (Extremes)
\(10 \times 12 = 120\) (Means)
\(120 = 120\), so it is a proportion.
Solving Proportion
Solving the proportion means finding the unknown value in the proportion.
Example 2 (Proportion)
Solve each proportion:
Solution
Life Applications on Proportion
Example 3 (Proportion)
A car consumes 3L of gasoline to travel 33 km. How many liters does it need for 121 km?
Solution
\(\frac{X}{121} = \frac{3}{33} \implies X = \frac{3 \times 121}{33} = 11\)
The car needs 11 liters of gasoline.
Graphical Representation of Proportion
- If plotted points lie on a straight line passing through the origin, the relationship is a proportion.
- If not, the relationship is not a proportion.
Example 4 (Proportion)
Determine if the distance is proportional to the time.
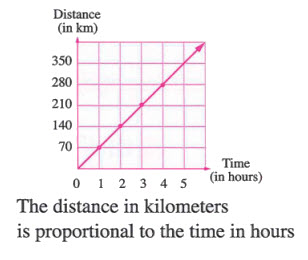
Proportional: The graph is a straight line through the origin.
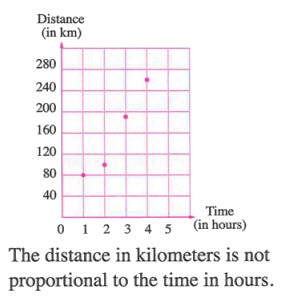
Not Proportional: The graph is not a straight line.