Factorizing a Number to its Prime Factors
Learn 1: Identify the prime factors of a whole number
Remember
A prime number
is a whole number that has exactly two different factors, 1 and itself.
Examples for prime numbers: 2, 3, 5, 7, 11, 13, 17
A composite number
is a whole number that has more than two factors.
Examples for composite numbers: 4, 6, 9, 12, 25, 30
How can you write a number as a product of its prime factors?
Every composite number can be written as a product of its prime factors. This product is called the prime factorization of a number. You can use a "factor tree" to find the prime factorization.
Example 1
Find the prime factorization for each of the following numbers.
Solution
a. Factor tree for 36
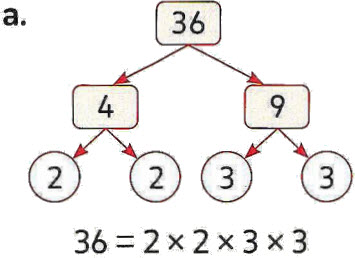
36 = 2 × 2 × 3 × 3
b. Factor tree for 28

28 = 2 × 2 × 7
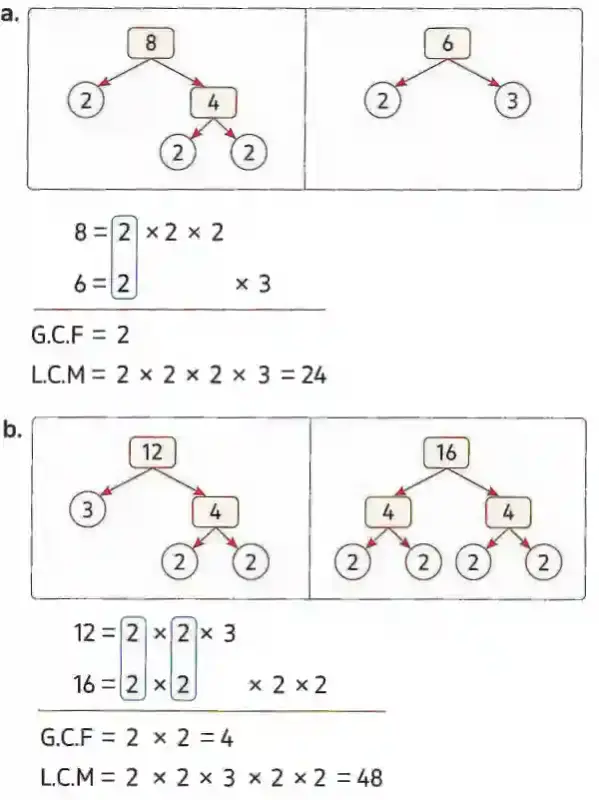
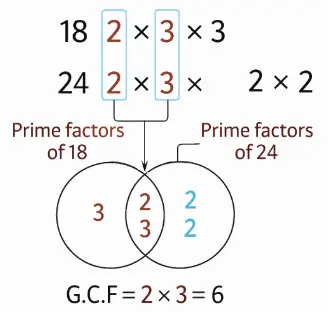
Learn 2: How can you find the greatest common factor (G.C.F)?
Remember
The greatest common factor (G.C.F) of two numbers is the greatest number that is a factor of both.
First way: using prime factorization
Factorize each number to its prime factors.
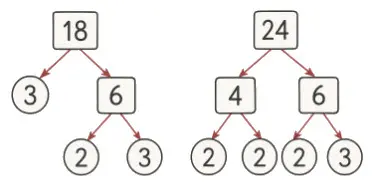
Find the common prime factors.
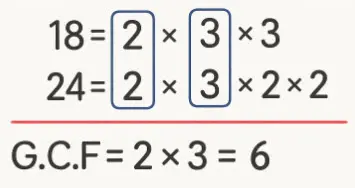
Find the product of these common prime factors.
G.C.F = 2 × 3 = 6
Second way: using Venn diagram
Factorize each number to its prime factors.
Find the common prime factors and write them in the common area in Venn diagram.
Find the product of these common prime factors.
Note
- Venn diagram can be used to compare similarities and differences between items.
- Where the circles overlap is where information is shared.
Learn 3: How can you find the least common multiple (L.C.M)?
Remember
The least common multiple (L.C.M) is the smallest multiple (other than 0) that two or more numbers have in common.
First way using prime factorization
Find all the prime factors of each of the given numbers.
Array prime factorization of each number such that the similar factors lie on the same column.
Take a factor from each column, then find their product which is the L.C.M
.webp)
Second way using Venn diagram

L.C.M is the product of all prime factors which are in Venn diagram.
L.C.M = 2 × 3 × 3 × 2 × 2 = 72
How can you find [L.C.M] and [G.C.F] of two relatively prime numbers?
The relatively prime numbers are numbers whose only common factor is 1.
For Example:
8 and 9 are two composite numbers.
8 = 2 × 2 × 2
9 = 3 × 3
Then, G.C.F = 1 and L.C.M = 2 × 2 × 2 × 3 × 3 = 72
Then, 8 and 9 are two relatively prime numbers.
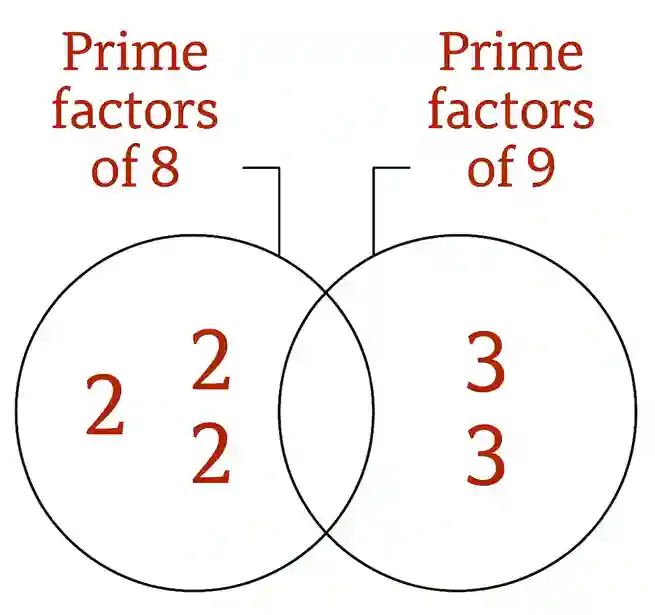
Note that:
Since the common area is empty, you can draw two distance circles as:
Example 1
Find G.C.F and L.C.M of 4 and 9. Are 4 and 9 two relatively prime numbers? Why?
Solution
4 = 2 × 2
9 = 3 × 3
G.C.F = 1
L.C.M = 2 × 2 × 3 × 3 = 36
4 and 9 are two relatively prime numbers because G.C.F of them = 1
Example 2
Find G.C.F and L.C.M of each of the following:
Solution